Angesichts der Tatsache, dass Binärsysteme für die Existenz von Computern so fundamental sind, ist es merkwürdig, dass wir das Thema nie zuvor behandelt haben - heute hatte ich gedacht, ich würde einen kurzen Überblick darüber geben, was Binär bedeutet und wie es in Computern verwendet wird . Wenn Sie sich schon immer gefragt haben, was der Unterschied zwischen 8-Bit, 32-Bit und 64-Bit wirklich ist und warum es wichtig ist - dann lesen Sie weiter!
Was ist binär? Der Unterschied zwischen Base 10 und Base 2
Die meisten von uns sind in einer Basis-10-Welt von Zahlen aufgewachsen, womit ich meine, dass wir 10 'Basis'- Zahlen ( 0-9 ) haben, aus denen wir alle anderen Zahlen ableiten. Sobald wir diese erschöpft haben, bewegen wir uns einen Einheitslevel nach oben - 10er, 100er, 1000er - diese Form des Zählens wird von Geburt an in unseren Gehirnen gehämmert. Tatsächlich haben wir erst ab der Römerzeit angefangen, in der Basis 10 zu zählen. Davor war die Basis 12 am einfachsten, und die Leute benutzten ihre Fingerknöchel, um zu zählen.
Wenn wir Basis 10 in der Grundschule lernen, schreiben wir die Einheiten oft so aus:
So besteht die Zahl 1990 tatsächlich aus 1 x 1000, 9 x 100, 9 x 10 und 0 x 1 . Ich bin mir sicher, dass ich Base 10 nicht weiter erklären muss.
Aber was wäre, wenn wir statt einer vollständigen Auswahl von 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 als Basiszahlen arbeiten würden - was wäre, wenn wir nur 0 und 1 hätten . Dies nennt man Basis 2 ; und es wird auch allgemein als binär bezeichnet . In einer binären Welt kannst du nur 0, 1 zählen - dann musst du zur nächsten Einheitsebene gehen.
Zählen in Binär
Es hilft immens, wenn wir beim Lernen von Binärdateien die Einheiten ausschreiben. In diesem Fall, anstatt jede zusätzliche Einheit mit 10 zu multiplizieren, wird sie mit 2 multipliziert, was uns 1, 2, 4, 8, 16, 32, 64 ergibt ... Um zu berechnen, können wir sie folgendermaßen ausschreiben :
Mit anderen Worten, der am weitesten rechts liegende Wert in einer Binärzahl gibt an, wie viele Einsen. Die nächste Ziffer links davon steht für die Anzahl der 2er. Der nächste steht für wie viele 4 ... und so.
Mit diesem Wissen können wir eine Zählungstabelle in binärer Form erstellen, mit dem äquivalenten Wert von 10 auf der linken Seite.
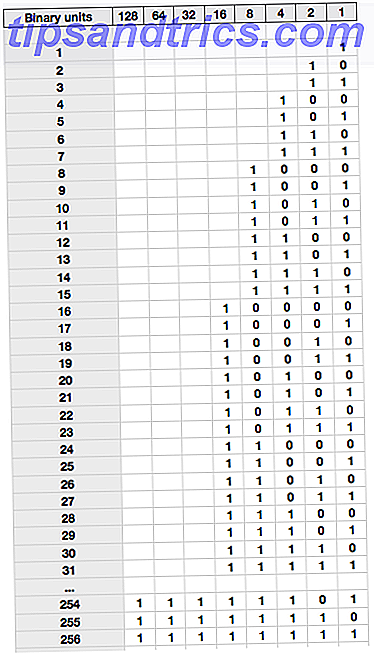
Verbringen Sie einen Moment damit, bis Sie genau sehen können, warum 25 als 11001 geschrieben wird. Sie sollten es als 16 + 8 + 1 = 25 aufschlüsseln können.
Rückwärts arbeiten - Basis 10 binär
Sie sollten jetzt in der Lage sein, herauszufinden, welchen Wert eine Binärzahl hat, indem Sie eine ähnliche Tabelle zeichnen und jede Einheit multiplizieren. Um eine reguläre Basis 10-Nummer in eine binäre zu wechseln, ist ein wenig mehr Aufwand erforderlich. Der erste Schritt besteht darin, die größte binäre Einheit zu finden, die in die Zahl passt. Wenn wir zum Beispiel 35 machen, dann ist die größte Zahl aus dieser Tabelle, die in 35 passt, 32, also hätten wir in dieser Spalte eine 1. Wir haben dann einen Rest von 3 - was eine 2 und dann schließlich eine 1 benötigen würde . Also bekommen wir 100011 .
8-Bit, Bytes und Oktetts
Die Tabelle, die ich oben gezeigt habe, ist 8-Bit, weil wir für unsere Binärzahl maximal 8 Nullen und Einsen haben. Daher ist die maximale Anzahl, die wir möglicherweise darstellen können, 11111111 oder 255 . Um eine beliebige Zahl von 0-255 darzustellen, benötigen wir daher mindestens 8 Bits. Oktett und Byte ist einfach eine andere Art, 8 Bits zu sagen. Daher 1 Byte = 8 Bits .
32 vs 64-Bit-Computing
Heutzutage hören Sie oft die Begriffe 32-Bit- und 64-Bit-Versionen von Windows, und Sie wissen vielleicht, dass 32-Bit-Windows nur bis zu 4 Gigabyte RAM unterstützen kann . Warum ist das so?
Es kommt auf die Speicheradressierung an. Jedes Speicherbit benötigt eine eindeutige Adresse, um darauf zugreifen zu können. Wenn wir ein 8-Bit- Speicheradressierungssystem hätten, könnten wir nur maximal 256 Bytes Speicher haben. Mit einem 32-Bit- Speicheradressierungssystem ( stellen Sie sich vor, die obige Tabelle auf 32 Binäreinheitsspalten zu erweitern ), können wir überall bis zu 4.294.967.296 gehen ? 4 Milliarden Bytes oder mit anderen Worten - 4 GIGA- Bytes. 64-Bit- Computing beseitigt diese Grenze im Wesentlichen, indem es uns bis zu 18 Trillionen verschiedene Adressen gibt - eine Zahl, die die meisten von uns einfach nicht verstehen können.
IPv4-Adressierung
Die neueste Sorge in der Computerwelt dreht sich alles um IP-Adressen IPv6 & The Coming ARPAgeddon [Technologie erklärt] IPv6 & The Coming ARPAgeddon [Technologie erklärt] Lesen Sie mehr, insbesondere IPv4- Adressen, wie diese:
- 192.168.0.1
- 200.187.54.22
Sie bestehen tatsächlich aus 4 Zahlen, von denen jede einen Wert von bis zu 255 darstellt. Können Sie raten, warum? Ja, die ganze Adresse wird durch 4 Oktette repräsentiert (insgesamt 32 Bits ). Dies schien eine schreckliche Menge möglicher Adressen ( ungefähr 4 Milliarden tatsächlich ) zu der Zeit, als das Internet erfunden wurde, aber wir sind schnell erschöpft, jetzt wo alles in unserem Leben verbunden werden muss. Um dies zu lösen, verwendet das neue IPv6 insgesamt 128 Bits, was uns ungefähr 340 Unzenzillionen ( 38 Nullen am Ende ) zur Verfügung stellt, mit denen man spielen kann.
Ich werde es für heute dort lassen, damit ich zu meinem ursprünglichen Ziel zurückkehren kann, nämlich das nächste Arduino-Tutorial zu schreiben - in dem wir uns ein Bit-Shift-Register ausgiebig zunutze machen. Ich hoffe, Ihnen heute ein grundlegendes Verständnis davon zu geben, wie binär für Computer so wichtig ist, warum die gleichen Zahlen immer wieder auftauchen und warum die Anzahl der Bits, die wir darstellen müssen, eine endliche Grenze für Speichergröße, Bildschirmgröße und mögliche Farbe darstellt Werte oder eindeutige IP-Adressen, die uns zur Verfügung stehen. Beim nächsten Mal werden wir uns mit binären Logikberechnungen beschäftigen, die so ziemlich alles sind , was ein Computerprozessor macht, und auch, wie Computer negative Zahlen darstellen können.
Bemerkungen? Verwechslung? Hast du meine Erklärung leicht verstanden? Wie auch immer, bitte kontaktieren Sie uns in den Kommentaren. Ich werde dich mit einem binären Witz verlassen!
Es gibt nur 10 Arten von Menschen auf der Welt: diejenigen, die Binär verstehen, und diejenigen, die dies nicht tun.
Bildnachweis: Shutterstock